It is easy to confuse what K is used for with what it actually means. K is useful for measuring a material’s resistance to fracture starting at a sharp-tipped crack. However, K is defined as a measurement of the magnitude of stress distribution around a sharp crack tip in a linear-elastic solid. K only has meaning in the context of materials that can be expected to form a certain distribution of stress around a sharp crack tip!
So if we have something that is predominantly linear-elastic (high-strength steels, glass, etc.) and it contains a sharp-tipped crack, then the stress distribution around that crack can be given in terms of this parameter we call K. The stress distributions for a crack in tension perpendicular to the crack faces (aka Mode I loading) are:
$$\sigma _{\text{yy}}=\frac{K
}{\sqrt{2 \pi r}} \cos (\theta ) \left(\sin \left(\frac{\theta }{2}\right) \sin \left(\frac{3 \theta }{2}\right)+1\right)$$
$$\sigma _{\text{xx}}=\frac{K
}{\sqrt{2 \pi r}}
\cos (\theta ) \left(1-\sin \left(\frac{\theta }{2}\right) \sin \left(\frac{3 \theta }{2}\right)\right) $$
$$\sigma _{\text{xy}}=\frac{K
}{\sqrt{2 \pi r}} \left(\sin \left(\frac{\theta }{2}\right) \cos \left(\frac{\theta }{2}\right) \cos \left(\frac{3 \theta }{2}\right)\right)$$
These plots show how the stress distribution looks for a stress intensity factor of K = 1 MPa √m.
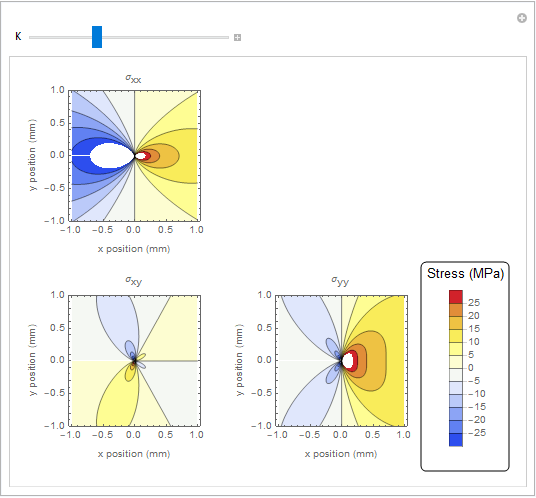
Stress distribution for a stress intensity factor of K = 1 MPa √m. The crack tip is located at (0,0) and the crack follows the x-axis along x < 0.

Stress distribution for a stress intensity factor of K = 2 MPa √m. Note that I kept the same scale so that we can see the effect on the spatial distribution.
Hopefully, this helps illustrate what the stress intensity factor, K, means in a mathematical sense. Though K is useful for measuring fracture toughness, it is only applicable for sharp crack tips in linear-elastic materials that exhibit stress distributions similar to what I have shown here.
Note that these solutions are approximations: they are the first, most significant term of a summation. But K is still a very useful parameter for materials that obey linear-elastic fracture mechanics.
I created a live-view applet for Wolfram Cloud, but it wasn’t playing nice with the cloud, hence my screenshots above. In the event I get it working, I’ll put it here.
Ce qui est simple est toujours faux. Ce qui ne l’est pas est inutilisable.
Paul Valéry
What is simple is always wrong. What is not is unusable.

